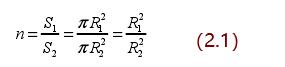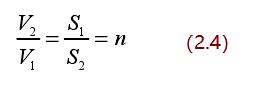縮徑式渦街流量計的縮徑結構
圖 2.1 是縮徑式渦街流量計的縮徑結構的示意圖,它包括收縮段、穩(wěn)定段、測量段。穩(wěn)定段是收縮段入口前的大口徑管道,測量段是收縮段出口后的小口徑管道,發(fā)生體和傳感器安裝在測量段。
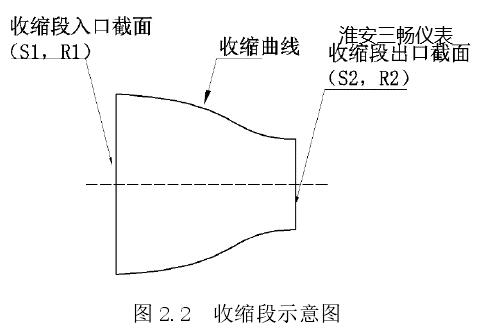
收縮段是縮徑結構的重要組成部分,圖 2.2 是收縮段的示意圖。收縮段由收縮曲線和收縮比兩部分組成。收縮曲線是指從大管徑過渡到小管徑的壁面線條。收縮比是收縮段入口截面面積與出口截面面積之比,其計算公式如下:
式(2.1)中,n 是收縮比,S1 是收縮段入口面積,R1 是收縮段入口截面半徑,S2是收縮段出口面積,R2 是收縮段出口截面半徑。
流體的連續(xù)性定理描述了流體流經不同截面的管道時流速與截面面積的關系,其內容是:當流體連續(xù)不斷地流過管道,單位時間內流過管道各個截面的流體的體積或質量都相等。這一定理可用式(2.2)表示:
A1v1 =A2v2 (2.2)
式(2.2)中,A1是流體流入截面的面積,v1 是流體在流入截面時的速度,A2是流體流出截面的面積,v2 是流體在流出截面時的速度。
收縮段中的流體同樣滿足連續(xù)性定理。假設收縮段入口截面上的流體流速為V1,收縮段入口截面的面積為 S1,收縮段出口截面上的流體流速為 V2,收縮段出口截面面積為 S2,有:
S1V1 =S2V2 (2.3)
聯(lián)立式(2.1)、(2.3)可得:
可知,流體在收縮段出口的流速是其在收縮段入口流速的 n 倍,n 即是收縮段的收縮比。這也是縮徑式渦街流量計使小流量變大,實現(xiàn)寬量程比的理論基礎。