在實際工業現場中雙彎管的應用比較普遍,由于空間90 雙彎管會在測量管道中產生渦流和回流,從而對超聲波流量計的測量精度造成不利的影響。應用CFD 數值仿真分析測量管道內流場分布情況,可以更準確的獲得測量結果。圖4.8 為空間90 雙彎管計算幾何模型。其中進口管段直管 D=100mm,測量段管道直管 D1=60mm,雙彎管彎曲半徑 R=1.5D,L1為兩個彎管之間的直管段距離,
本文定義 L1=2D,L 為彎管出口與流量計進口之間的直管段長度,本文 L 分別取 2D、4D、6D、8D、10D、20D、30D 和 40D。在 Fluent 中仿真流量定義為Q=0.1m3/h、0.2m3/h、0.4m3/h、1m3/h、3m3/h、5m3/h、10m3/h、30m3/h、60m3/h、90m3/h 和 120m3/h,網格采用非結構型混合網格,直管段采用結構型網格,彎管和測量段采用非結構網格,網格總數量為 200 萬左右;Fluent 數值仿真中邊界條件等參數設置與平面90 單彎管相同。
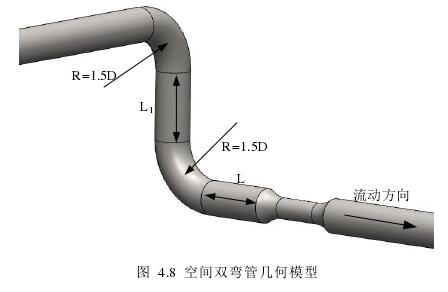
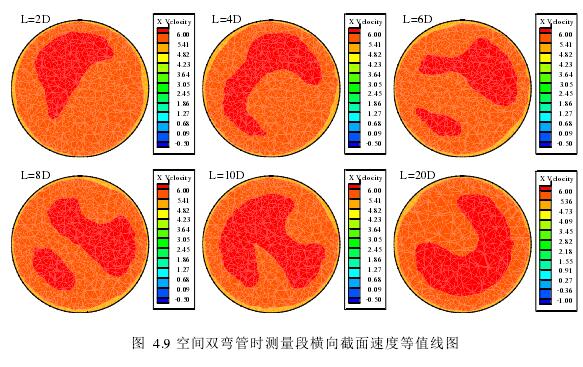
圖 4.9 為 DN100 超聲波流量計上游阻流件為空間雙彎管時,測量段橫向截面速度等值線圖。圖中為流量均為 Q=60m3/h 時,彎管出口與流量計入口之間的距離分別為 L=2D、4D、6D、8D、10D 和 20D。由于空間雙彎管會使管道中存在渦流或回流等現象,因此導致超聲波流量計測量段內速度分布不均勻,非理想流場速度分布引起流量測量誤差。圖 4.9 得出結論:在 L=2D 和 4D 時渦流所引起的速度分布不均勻情況非常嚴重,隨著彎管與測量段之間的距離越來越大時,空間雙彎管所引起的速度場分布不均勻情況有所減弱。因此從速度分布等值線圖中可以得出隨著彎管與測量段之間的距離越來越大,彎管所引起的測量誤差應該越來越小。
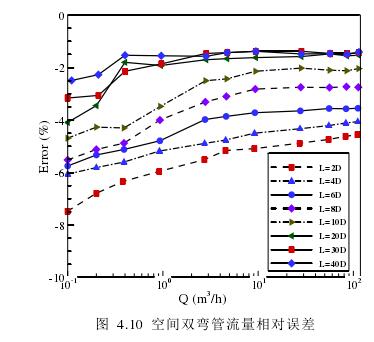
圖 4.10 所示空間90 雙彎管所引起的流量相對誤差同樣是以直管段 40D 時流量誤差為基準,應用公式(4-3)計算得出。其中橫坐標為流量測量值,采用對數表達方式,以方便觀測小流量時變化趨勢,縱坐標為流量相對誤差,不同曲線表示兩個彎管之間直管段距離為 L1=2D,不同距離 L 時的流量相對誤差。
從圖 4.10 得出結論:當距離 L 相同時,即同一條曲線上,當流量為Q=5m3/h~120m3h 時 流 量 相 對 誤 差 趨 于 直 線 , 無 明 顯 變 化 ; 當 流 量 為0.1m3/h~5m3/h 時,隨著流量的增大,空間雙彎管所引起的流量相對誤差逐漸減小。對于相同流量點不同距離 L 時,距離 L 為 20D、30D 和 40D 時,同流量相對誤差大小相近;在彎管與測量段之間距離較小時,渦流對測量準確度的影響較大,當彎管與測量段之間距離增大到 20D 以后,渦流對測量準確度的影響無明顯變化,但仍會產生流量誤差。這正好與上圖 4.9 所示測量段橫截面上速度分布等值線圖結論相符。